832. Возрастающая подпоследовательность
Даны n целых чисел x1, x2,
..., xn. Вычеркните из них
наименьшее количество чисел так, чтобы оставшиеся шли в порядке возрастания.
Вход. В первой строке находится число n (1 ≤ n ≤ 10 000).
Во второй строке заданы числа x1,
x2, ..., xn (1 ≤ xi ≤ 60 000).
Выход. Выведите в
первой строке количество невычеркнутых чисел, во второй – сами невычеркнутые
числа в исходном порядке. Если вариантов несколько, то выведите любой.
|
Пример
входа |
Пример
выхода |
|
6 2 5 3 4 6 1 |
4 2 3 4 6 |
РЕШЕНИЕ
наибольшая
возрастающая подпоследовательность
Анализ алгоритма
В задаче следует найти и вывести наибольшую возрастающую
подпоследовательность.
Для каждого элемента xi (1 ≤ i ≤ n) найдем длину НВП, которая заканчивается в xi. Все эти значения сохраним в массиве L. Этой информации достаточно,
чтобы за линейное время найти саму НВП. Длина НВП равна максимальному числу k в массиве L. Пусть это наибольшее
число k находится в индексе pos. Тогда НВП заканчивается числом xpos. Уменьшаем pos до тех пор, пока L[pos] не станет равным k – 1. Текущее xpos будет предпоследним элементов в НВП. И так дальше
продолжаем двигать индекс pos к
началу массива L, останавливаясь на первых позицях, для которых L[pos] = k – 2, …, L[pos] = 0.
Теорема. Рассмотрим индексы i1 < i2
< …< im, для которых
L[i1] = L[i2] = …= L[im]. Тогда последовательность
xi1, xi2, …, xim является убывающей.
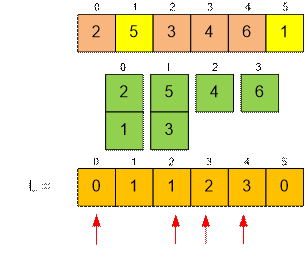
Пример
Расклад пасьянса имеет вид:
L[i] содержит номер
стопки, в которую будет положена карта xi (нумерация стопок
начинается с нуля).
Реализация алгоритма
Объявим рабочие массивы.
#define MAX 60001
int x[MAX], lis[MAX], L[MAX];
Вывод НВП.
void PrintSeq(int
pos)
{
if (size <
0) return;
while(L[pos]
!= size) pos--;
size--; PrintSeq(pos-1);
printf("%d
",x[pos]);
}
Основная часть программы. Читаем
входную последовательность.
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d",&x[i]);
Заполняем рабочие массивы.
for (len = i = 0; i < n; i++)
{
pos = lower_bound(lis,lis+len,x[i]) - lis;
lis[pos] = x[i];
L[i] = pos;
if (pos ==
len) len++;
}
Выводим наибольшую возрастающую
подпоследовательность.
printf("%d\n",len); size = len - 1;
PrintSeq(n-1);
printf("\n");